矢量交叉积计算器
矢量 X
矢量 Y
如何使用交叉积计算器?
矢量交叉积计算器使用起来非常简单,请按照以下步骤找出交叉积:- 步骤 1 : 在输入框中输入给定的向量 X 和 Y 系数。
- 步骤 2 : 单击“获取计算”按钮以获取交叉积的值。
- 步骤 3 : 最后,您将获得两个向量之间的交叉乘积值以及详细的分步解决方案。
什么是交叉积?
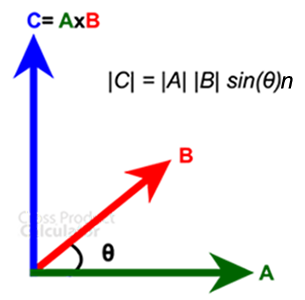
两个向量 a 和 b 之间的乘积称为“交叉乘积”。它只能在三维空间中表达,而不能在二维空间中表达。它由“a ⨯ b”(表示十字 b)表示。
两个向量的结果称为“c”,它垂直于两个向量 a 和 b,其中 θ 是两个向量之间的角度。它的方向由右手定则给出,大小由平行四边形的面积给出。
交叉乘积公式
a x b = |a| |b| sin (θ) n
- | a |和 | b | 是两个向量的长度。
- θ 是两个矢量 A 和 B 之间的角度(范围在 0° 到 180° 之间)。
- n 是垂直于向量 A 和 B 的单位向量。
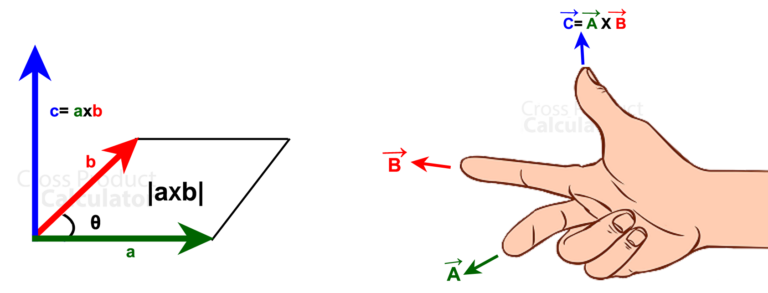
如果向量 a 和 b 平行,则它们的叉积为零。
向量 c 的方向可以简单地通过右手拇指法则知道,其中-
食指应该朝向 a 的方向。 中指应朝 b 的方向。 交叉乘积公式比通常的公式复杂一些。
在 3D 空间中计算矢量之间的角度可能会变得过于复杂;而且,如果我们只想知道如何计算两个向量之间的交叉乘积,那么可能不值得麻烦。相反,让我们探索一种更直接、更实用的方法来使用不同的叉积公式计算向量交叉积。
这个新公式利用 3D 矢量分解为三个组成部分。这种技术是描述和操作向量的一种非常常见的方法,其中每个分量表示空间中的一个方向,伴随它的数字表示向量在特定方向上的长度。通常,我们正在处理的 3-D 空间的三个维度被命名为 x、y 和 z,分别由酉向量 i、j 和 k 表示。
按照这个命名法,我们可以用这三个酉向量的总和来表示每个向量。为了简洁起见,通常省略向量,但仍然是隐含的,并且对交叉乘积结果有很大影响。因此,向量 v 可以表示为:v = (3i + 4j + 1k),或者简而言之:v = (3, 4, 1),其中数字的位置很重要。使用这种符号,我们现在可以了解如何计算两个向量的叉积。
我们将两个向量称为:v = (v₁, v₂, v₃) 和 w = (w₁, w₂, w₃)。对于这两个向量,公式如下所示:
v × w = (v₂w₃ - v₃w₂, v₃w₁ - v₁w₃, v₁w₂ - v₂w₁)
这个结果可能看起来像是每个向量的分量之间的随机运算集合,但实际上并没有更远。对于那些想知道这一切来自哪里的人,我们鼓励您自己发现它。您需要做的就是从表示为:v = v₁i + v₂j + v₃k 和 w = w₁i + w₂j + w₃k 的两个向量开始,然后将向量的每个分量乘以另一个分量的所有分量。
作为一个小提示,我们可以告诉你,当做向量的叉积乘以数字时,结果是数字乘以向量之间的叉积的“正则”乘积。记住平行向量(以及向量与自身的交积)的交叉乘积总是等于 也会派上用场。